The Case of Noninvertible Follows From Continuity

Abstract

Let 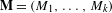$\mathbf{M}=(M_{1},\ldots ,M_{k})$ be a tuple of real 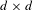$d\times d$ matrices. Under certain irreducibility assumptions, we give checkable criteria for deciding whether 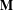$\mathbf{M}$ possesses the following property: there exist two constants 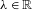$\unicode[STIX]{x1D706}\in \mathbb{R}$ and 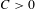$C>0$ such that for any 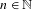$n\in \mathbb{N}$ and any 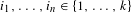$i_{1},\ldots ,i_{n}\in \{1,\ldots ,k\}$ , either 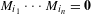$M_{i_{1}}\cdots M_{i_{n}}=\mathbf{0}$ or $C^{-1}e^{\unicode[STIX]{x1D706}n}\leq \Vert M_{i_{1}}\cdots M_{i_{n}}\Vert \leq Ce^{\unicode[STIX]{x1D706}n}$ , where $\Vert \cdot \Vert$ is a matrix norm. The proof is based on symbolic dynamics and the thermodynamic formalism for matrix products. As applications, we are able to check the absolute continuity of a class of overlapping self-similar measures on 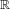$\mathbb{R}$ , the absolute continuity of certain self-affine measures in 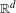$\mathbb{R}^{d}$ and the dimensional regularity of a class of sofic affine-invariant sets in the plane.

References

Barral, J. and Feng, D.-J. . Multifractal formalism for almost all self-affine measures. Comm. Math. Phys. 318(2) (2013), 473–504.Google Scholar

Bedford, T. . Crinkly curves, Markov partitions and dimension. PhD Thesis, University of Warwick, 1984.Google Scholar

Blondel, V. D. and Tsitsiklis, J. N. . When is a pair of matrices mortal? Inform. Process. Lett. 63(5) (1997), 283–286.Google Scholar

Blondel, V. D. and Tsitsiklis, J. N. . The boundedness of all products of a pair of matrices is undecidable. Systems Control Lett. 41(2) (2000), 135–140.Google Scholar

Blondel, V. D. and Tsitsiklis, J. N. . A survey of computational complexity results in systems and control. Automatica J. IFAC 36(9) (2000), 1249–1274.Google Scholar

Cao, Y.-L. , Feng, D.-J. and Huang, W. . The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20(3) (2008), 639–657.Google Scholar

Cassaigne, J. , Halava, V. , Harju, T. and Nicolas, F. . Tighter undecidability bounds for matrix mortality, zero-in-the-corner problems, and more. Preprint, 2014, arXiv:1404.0644.Google Scholar

Deng, Q.-R. , He, X.-G. and Lau, K.-S. . Self-affine measures and vector-valued representations. Studia Math. 188(3) (2008), 259–286.Google Scholar

Falconer, K. J. . Fractal Geometry: Mathematical Foundations and Applications, 2nd edn. John Wiley & Sons, Inc., Hoboken, NJ, 2003.Google Scholar

Fan, A.-H. , Lau, K.-S. and Rao, H. . Relationships between different dimensions of a measure. Monatsh. Math. 135(3) (2002), 191–201.Google Scholar

Feng, D.-J. . Smoothness of the L ^q -spectrum of self-similar measures with overlaps. J. Lond. Math. Soc. (2) 68(1) (2003), 102–118.Google Scholar

Feng, D.-J. . The variational principle for products of non-negative matrices. Nonlinearity 17(2) (2004), 447–457.Google Scholar

Feng, D.-J. . Equilibrium states for factor maps between subshifts. Adv. Math. 226(3) (2011), 2470–2502.Google Scholar

Feng, D.-J. and Hu, H. . Dimension theory of iterated function systems. Comm. Pure Appl. Math. 62(11) (2009), 1435–1500.Google Scholar

Feng, D.-J. and Käenmäki, A. . Equilibrium states of the pressure function for products of matrices. Discrete Contin. Dyn. Syst. 30(3) (2011), 699–708.Google Scholar

Feng, D.-J. and Lau, K.-S. . The pressure function for products of non-negative matrices. Math. Res. Lett. 9(2–3) (2002), 363–378.Google Scholar

Feng, D.-J. and Lau, K.-S. . Multifractal formalism for self-similar measures with weak separation condition. J. Math. Pures Appl. (9) 92(4) (2009), 407–428.Google Scholar

Hare, K. E. , Hare, K. G. and Ng, M. K. S. . Local dimensions of measures of finite type II — measures without full support and with non-regular probabilities. Canad. J. Math. 70(4) (2018), 824–867.Google Scholar

Hare, K. G. , Morris, I. D. , Sidorov, N. and Theys, J. . An explicit counterexample to the Lagarias–Wang finiteness conjecture. Adv. Math. 226(6) (2011), 4667–4701.Google Scholar

Horn, R. A. and Johnson, C. R. . Matrix Analysis. Cambridge University Press, Cambridge, 1985.Google Scholar

Hutchinson, J. E. . Fractals and self-similarity. Indiana Univ. Math. J. 30(5) (1981), 713–747.Google Scholar

Jia, R.-Q. , Lau, K.-S. and Zhou, D.-X. . L _p solutions of refinement equations. J. Fourier Anal. Appl. 7(2) (2001), 143–167.Google Scholar

Jungers, R. . The Joint Spectral Radius: Theory and Applications (Lecture Notes in Control and Information Sciences, 385) . Springer, Berlin, 2009.Google Scholar

Käenmäki, A. . On natural invariant measures on generalised iterated function systems. Ann. Acad. Sci. Fenn. Math. 29(2) (2004), 419–458.Google Scholar

Kenyon, R. and Peres, Y. . Hausdorff dimensions of sofic affine-invariant sets. Israel J. Math. 94 (1996), 157–178.Google Scholar

Kenyon, R. and Peres, Y. . Measures of full dimension on affine-invariant sets. Ergod. Th. & Dynam. Sys. 16(2) (1996), 307–323.Google Scholar

Lagarias, J. C. and Wang, Y. . The finiteness conjecture for the generalized spectral radius of a set of matrices. Linear Algebra Appl. 214 (1995), 17–42.Google Scholar

Lagarias, J. C. and Wang, Y. . Integral self-affine tiles in R ⁿ . I. Standard and nonstandard digit sets. J. Lond. Math. Soc. (2) 54(1) (1996), 161–179.Google Scholar

Lalley, S. P. . Random series in powers of algebraic integers: Hausdorff dimension of the limit distribution. J. Lond. Math. Soc. (2) 57(3) (1998), 629–654.Google Scholar

Lau, K.-S. and Ngai, S.-M. . Multifractal measures and a weak separation condition. Adv. Math. 141(1) (1999), 45–96.Google Scholar

Lau, K.-S. , Ngai, S.-M. and Rao, H. . Iterated function systems with overlaps and self-similar measures. J. Lond. Math. Soc. (2) 63(1) (2001), 99–116.Google Scholar

Lind, D. and Marcus, B. . An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar

Lo, C. H. . Dimensional regularity of some sofic affine sets. Master Thesis, The Chinese University of Hong Kong, 2012.Google Scholar

Mattila, P. . Geometry of Sets and Measures in Euclidean Spaces (Cambridge Studies in Advanced Mathematics, 44) . Cambridge University Press, Cambridge, 1995.Google Scholar

McMullen, C. . The Hausdorff dimension of general Sierpiński carpets. Nagoya Math. J. 96 (1984), 1–9.Google Scholar

Morris, I. D. . Ergodic properties of matrix equilibrium states. Ergod. Th. & Dynam. Sys. 38(6) (2018), 2295–2320.Google Scholar

Ngai, S.-M. and Wang, Y. . Hausdorff dimension of self-similar sets with overlaps. J. Lond. Math. Soc. (2) 63(3) (2001), 655–672.Google Scholar

Nguyen, N. . Iterated function systems of finite type and the weak separation property. Proc. Amer. Math. Soc. 130(2) (2002), 483–487 (electronic).Google Scholar

Omladič, M. and Radjavi, H. . Irreducible semigroups with multiplicative spectral radius. Linear Algebra Appl. 251 (1997), 59–72.Google Scholar

Parry, W. . Intrinsic Markov chains. Trans. Amer. Math. Soc. 112 (1964), 55–66.Google Scholar

Paterson, M. S. . Unsolvability in 3 × 3 matrices. Stud. Appl. Math. 49 (1970), 105–107.Google Scholar

Peres, Y. , Schlag, W. and Solomyak, B. . Sixty years of Bernoulli convolutions. Fractal Geometry and Stochastics, II (Greifswald/Koserow, 1998) (Progress in Probability, 46) . Birkhäuser, Basel, 2000, pp. 39–65.Google Scholar

Popov, A. I. . On matrix semigroups bounded above and below. Linear Algebra Appl. 438(11) (2013), 4439–4447.Google Scholar

Protasov, V. Y. . Refinement equations with nonnegative coefficients. J. Fourier Anal. Appl. 6(1) (2000), 55–78.Google Scholar

Protasov, V. Y. . When do several linear operators share an invariant cone? Linear Algebra Appl. 433(4) (2010), 781–789.Google Scholar

Protasov, V. Y. and Voynov, A. S. . Matrix semigroups with constant spectral radius. Linear Algebra Appl. 513 (2017), 376–408.Google Scholar

Rockafellar, R. T. . Convex Analysis (Princeton Mathematical Series, No. 28) . Princeton University Press, Princeton, NJ, 1970.Google Scholar

Ruiz, V. . Dimension of homogeneous rational self-similar measures with overlaps. J. Math. Anal. Appl. 353(1) (2009), 350–361.Google Scholar

Shmerkin, P. . Overlapping self-affine sets. Indiana Univ. Math. J. 55(4) (2006), 1291–1331.Google Scholar

Shmerkin, P. . On the exceptional set for absolute continuity of Bernoulli convolutions. Geom. Funct. Anal. 24(3) (2014), 946–958.Google Scholar

Shmerkin, P. and Solomyak, B. . Absolute continuity of self-similar measures, their projections and convolutions. Trans. Amer. Math. Soc. 368(7) (2016), 5125–5151.Google Scholar

Solomyak, B. . On the random series ∑ ±𝜆 ⁿ (an Erdős problem). Ann. of Math. (2) 142(3) (1995), 611–625.Google Scholar

Walters, P. . An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar

Zerner, M. P. W. . Weak separation properties for self-similar sets. Proc. Amer. Math. Soc. 124(11) (1996), 3529–3539.Google Scholar

Zhou, D.-X. . The p-norm joint spectral radius for even integers. Methods Appl. Anal. 5(1) (1998), 39–54.Google Scholar

sumnerdoety1966.blogspot.com

Source: https://www.cambridge.org/core/journals/ergodic-theory-and-dynamical-systems/article/uniformity-of-lyapunov-exponents-for-noninvertible-matrices/FCCBD792610373379581BAF201E13283

Share this post